Как при каждом А решить систему уравнений?

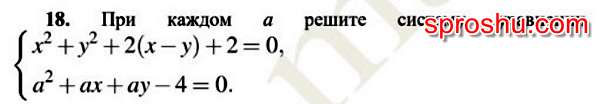
Что-то у Вас всё перемешано и перепутано.

Первое уравнение решается само по себе, без привлечения второго:

x^2 + y^2 + 2(x-y) + 2 =0;

x^2 + y^2 + 2x - 2y + 1+1 =0;

x^2 + 2x +1 + y^2 - 2y + 1 =0;

(x^2 + 2x +1) +(y^2 - 2y + 1) =0;

(x + 1)^2 +(y - 1)^2 =0.

Каждое из слагаемых - неотрицательно (либо положительно, либо равно нулю).

Сумма двух неотрицательных чисел равна нулю только если каждое из них равно нулю.

Наше уравнение распадается на два независимых уравнения:

(x + 1) =0, (y - 1) =0;

Очевидно, что х=-1, у=1.

Мы можем подставить эти значения во второе уравнение системы, и получить

a^2 - 4 = 0, откуда а=2 или а=-2.даже не связаны друг с другом. не зависят друг от друга

Как видно, что вопрос явно не для этого задания, или смешаны два разных задания.

Даже сам вопрос (в задании) сформулирован с ошибкой. "При каждом а решите систему уравнении". Если бы было "...систему уравнений...", то, по крайней мере с точки зрения русского языка, было бы правильно.

Выкиньте источник, откуда взято это задание (учебник, задачник, решебник или как это там у Вас называется), и никогда не пользуйтесь им.