
Bameschsa
7 год назад
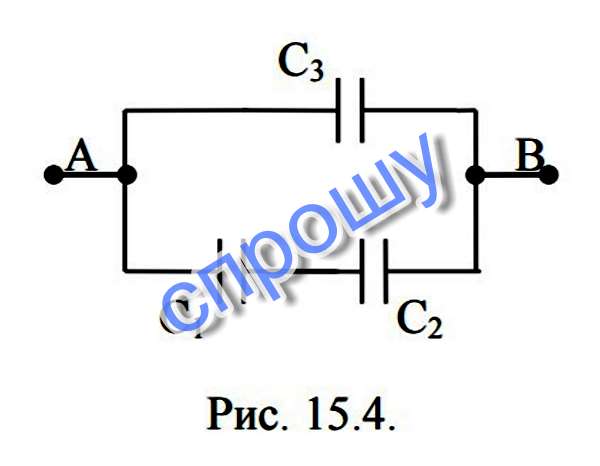
Батарея конденсаторов с вертикально расположенными
пластинами и с емкостями соответственно 5, 8 и 1 мкФ, изображенная на
рисунке 15.4, была заряжена от источника с напряжением 250 В, который
подключался к точкам А и В. а) Какую энергию получила батарея? б)
Каким станет напряжение на батарее, если после отключения ее от
источника второй конденсатор вертикально на половину погрузить в
трансформаторное масло с диэлектрической проницаемостью 2? Ответ:
127,5 мДж, 227 В.
ОТВЕТЫ

Биркин
Jul 5, 2019
А) Проводник между  и
и  – изолированный, так что:
– изолированный, так что:



Складываем:

Ёмкость на нижней ветке:

Энергия, аккумулированная на нижней ветке:

На верхней:

Во всей цепи:


 мДж ;
мДж ;
б) Верхняя половина второго конденсатора имеет половину его полной ёмкости. Нижняя половина второго конденсатора имеет половину ёмкости исходного, умноженную на диэлектрическую проницаемость. Итого обновлённая ёмкость второго конденсатора будет:

Короче говоря, ёмкость второго конденсатора увеличится, он наэлектризует, поляризует и втянет в себя масло, совершив работу. Так что второй конденсатор начнёт втягивать в себя и заряд по правому концу нижней ветки. Противоположный заряд перетечёт и по изолированному проводнику нижней ветки от первого ко второму конденсатору. И такой же заряд
по правому концу нижней ветки. Противоположный заряд перетечёт и по изолированному проводнику нижней ветки от первого ко второму конденсатору. И такой же заряд  перетечёт и по левой стороне цепи между третьим и первым конденсатором. Из-за этого изменятся и напряжения на конденсаторах, а напряжения верхней и нижней ветки, в конечном счете, должны быть одинаковыми.
перетечёт и по левой стороне цепи между третьим и первым конденсатором. Из-за этого изменятся и напряжения на конденсаторах, а напряжения верхней и нижней ветки, в конечном счете, должны быть одинаковыми.
Из-за увеличения ёмкости второго конденсатора, увеличится и ёмкость всей нижней ветки. Обновлённая ёмкость нижней ветки будет:

Однако суммарный заряд на точках исходного подключения останется прежним, именно он будет определять конечное напряжение. Заряд до погружения в масло можно посчитать, как:

Заряд после погружения в масло можно посчитать, как:

А поскольку заряд сохраняется, то:


 В .
В .
Складываем:
Ёмкость на нижней ветке:
Энергия, аккумулированная на нижней ветке:
На верхней:
Во всей цепи:
б) Верхняя половина второго конденсатора имеет половину его полной ёмкости. Нижняя половина второго конденсатора имеет половину ёмкости исходного, умноженную на диэлектрическую проницаемость. Итого обновлённая ёмкость второго конденсатора будет:
Короче говоря, ёмкость второго конденсатора увеличится, он наэлектризует, поляризует и втянет в себя масло, совершив работу. Так что второй конденсатор начнёт втягивать в себя и заряд
Из-за увеличения ёмкости второго конденсатора, увеличится и ёмкость всей нижней ветки. Обновлённая ёмкость нижней ветки будет:
Однако суммарный заряд на точках исходного подключения останется прежним, именно он будет определять конечное напряжение. Заряд до погружения в масло можно посчитать, как:
Заряд после погружения в масло можно посчитать, как:
А поскольку заряд сохраняется, то:
182
Смежные вопросы:
