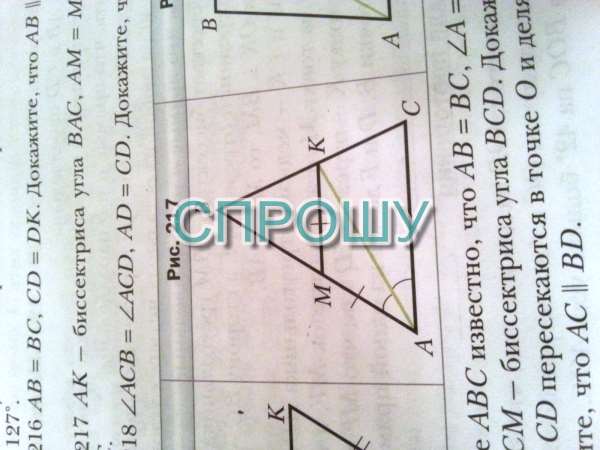
AK-биссектриса угла BAC, AM = MK. Докажите, что MK|| AC

Если АМ=МК, значит треугольник АМК равнобедренный и углы при основании АК у него равны ⇒ ∠МАК=∠АКМ.
Так как АК биссектриса ∠ВАС, то ∠КАС=∠МАК= ∠АКМ. Из равенства углов АКМ и КАС мы можем доказать параллельность МК и АС, так как эти углы внутренние накрест лежащие для этих прямых и секущей АК, если они равны это и есть признак параллельности прямых МК и АС.