
Zarad
7 год назад
Помогите с логарифмическом неравенством
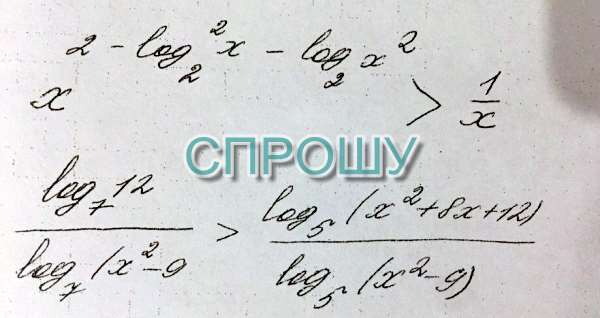
ОТВЕТЫ

Аврелиевич
Jun 29, 2019
1
ОДЗ
{xgt;0
{x≠1
x∈(0;10 U (1;∞)
x^(2-log²(2)-2log(2)xgt;x^-1
1)x∈(0;1) основание меньше 1,знак меняется
2-log²(2)x-2-2log(2)xlt;-1
log²(2)x-+2log(2)x-3gt;0
log(2)x=a
a²+2a-3gt;0
a1+a2=-2 U a1*a2=-3⇒a=-3 U a=1
alt;-3⇒log(2)xlt;-3⇒xlt;1/8
agt;1⇒log(2)xgt;1⇒xgt;2
x∈(0;1/8)
2)x∈(1;∞)
-3lt;alt;1⇒-3lt;log(2)xlt;1⇒1/8lt;xlt;2
x∈(1;2)
Ответ x∈(0;1/8) U (1;2)
2
ОДЗ
{x²-9gt;0
{x²+8x+12gt;0
(x-3)(x+3)gt;0
xlt;-3 U xgt;3
x1=x2=-8 U x1*x2=12⇒x1=-6 u x2=-2
xlt;-6 U xgt;-2
x∈(-∞;-8) U (3;∞)
Основание больше 1
log(x²-9)12gt;log(x²-9)(x²+8x+12)
x²+8x+12lt;12
x²+8xlt;0
x(x+8)lt;0
x=0 x=-8
-8lt;xlt;0
x∈(-∞;-8) U (3;∞)
ОДЗ
{xgt;0
{x≠1
x∈(0;10 U (1;∞)
x^(2-log²(2)-2log(2)xgt;x^-1
1)x∈(0;1) основание меньше 1,знак меняется
2-log²(2)x-2-2log(2)xlt;-1
log²(2)x-+2log(2)x-3gt;0
log(2)x=a
a²+2a-3gt;0
a1+a2=-2 U a1*a2=-3⇒a=-3 U a=1
alt;-3⇒log(2)xlt;-3⇒xlt;1/8
agt;1⇒log(2)xgt;1⇒xgt;2
x∈(0;1/8)
2)x∈(1;∞)
-3lt;alt;1⇒-3lt;log(2)xlt;1⇒1/8lt;xlt;2
x∈(1;2)
Ответ x∈(0;1/8) U (1;2)
2
ОДЗ
{x²-9gt;0
{x²+8x+12gt;0
(x-3)(x+3)gt;0
xlt;-3 U xgt;3
x1=x2=-8 U x1*x2=12⇒x1=-6 u x2=-2
xlt;-6 U xgt;-2
x∈(-∞;-8) U (3;∞)
Основание больше 1
log(x²-9)12gt;log(x²-9)(x²+8x+12)
x²+8x+12lt;12
x²+8xlt;0
x(x+8)lt;0
x=0 x=-8
-8lt;xlt;0
x∈(-∞;-8) U (3;∞)
98
