
Анастасия
7 год назад
Помогите с логарифмическом неравенством
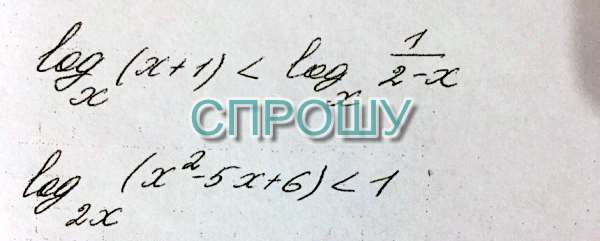
ОТВЕТЫ

Злоба
Jun 29, 2019
1
ОДЗ
{xgt;0
{x≠1
{x+1gt;0⇒xgt;-1
{2-xgt;0⇒xlt;2
x∈(0;1) U (1;2)
1)x∈(0;1) основание меньше 1
x+1gt;1/(2-x)
x+1-1/(2-x)gt;0
(2x+2-x²-x-1)/(2-x)gt;0
(-x²+x+1)/(2-x)gt;0
(x²-x-1)/(x-2)gt;0
x²-x-1=0
D=1+4=5
x1=(1-√5)/2 U x2=(1+√5)/2
x-2=0⇒x=2
_ + _ +
---------------(1-√5)/2----(0)----(1)---(1+√5)/2-------------(2)------------------
//////////
x∈(0;1)
2)x∈(1;2)
(x²-x-1)/(x-2)lt;0
_ + _ +
---------------(1-√5)/2--------(1)---(1+√5)/2-------------(2)------------------
///////////////////////////////////////
x∈((1+√5(/2;2)
Ответ x∈(0;1) U ((1+√5)/2;2)
2
ОДЗ
{xgt;0
{x≠1/2
{x²-5x+6gt;0⇒xlt;2 U xgt;3
x1+x2=5 U x1*x2=6⇒x1=2 U x2=3
x∈(0;1/2) (1/2;2) U (3;∞)
1)x∈(0;1/2) основание меньше 1
x²-5x+6gt;2x
x²-7x+6gt;0
x1+x2=7 U x1*x2=6
x1=1 U x2=6
xlt;1 U xgt;6
x∈(0;1/2)
2)x∈(1/2;2) U (3;∞)
x²-7x+6lt;0
1lt;xlt;6
x∈(1;2) U (3;6)
Ответ x∈(0;1/2) U (1;2) U (3;6)
ОДЗ
{xgt;0
{x≠1
{x+1gt;0⇒xgt;-1
{2-xgt;0⇒xlt;2
x∈(0;1) U (1;2)
1)x∈(0;1) основание меньше 1
x+1gt;1/(2-x)
x+1-1/(2-x)gt;0
(2x+2-x²-x-1)/(2-x)gt;0
(-x²+x+1)/(2-x)gt;0
(x²-x-1)/(x-2)gt;0
x²-x-1=0
D=1+4=5
x1=(1-√5)/2 U x2=(1+√5)/2
x-2=0⇒x=2
_ + _ +
---------------(1-√5)/2----(0)----(1)---(1+√5)/2-------------(2)------------------
//////////
x∈(0;1)
2)x∈(1;2)
(x²-x-1)/(x-2)lt;0
_ + _ +
---------------(1-√5)/2--------(1)---(1+√5)/2-------------(2)------------------
///////////////////////////////////////
x∈((1+√5(/2;2)
Ответ x∈(0;1) U ((1+√5)/2;2)
2
ОДЗ
{xgt;0
{x≠1/2
{x²-5x+6gt;0⇒xlt;2 U xgt;3
x1+x2=5 U x1*x2=6⇒x1=2 U x2=3
x∈(0;1/2) (1/2;2) U (3;∞)
1)x∈(0;1/2) основание меньше 1
x²-5x+6gt;2x
x²-7x+6gt;0
x1+x2=7 U x1*x2=6
x1=1 U x2=6
xlt;1 U xgt;6
x∈(0;1/2)
2)x∈(1/2;2) U (3;∞)
x²-7x+6lt;0
1lt;xlt;6
x∈(1;2) U (3;6)
Ответ x∈(0;1/2) U (1;2) U (3;6)
30
