
Siakveta
7 год назад
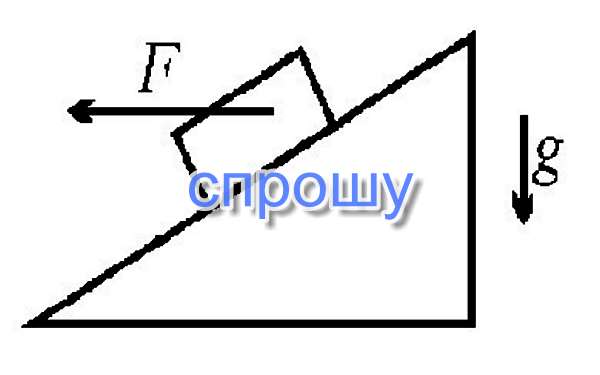
Брусок массы m лежит на плоскости, наклоненной
под углом α к горизонту. На него действует
горизонтальная сила F (см. рисунок). Определите
ускорение бруска. Коэффициент трения бруска о
плоскость M.
ОТВЕТЫ

Ioil
Jul 14, 2019
В задаче есть случаи, но надо сначала сказать что-нибудь точно
Спроецируем все силы на ось, перпендикулярную плоскости, предполагая, что тело все-таки лежит на ней, а не отрывается от нее внешней силой F

Итак, поскольку сила реакции опоры не может быть меньше нуля, находим первое ограничение на силу F

Поработаем в этом режиме. Сила F и сила тяжести стремятся двигать брусок вниз вдоль плоскости, значит сила трения направлена вверх вдоль плоскости. Тут также возможны два случая - тело покоится и тело стоит. Найдем в каком случае тело будет покоиться.

Сила трения не может превышать μN, поэтому

Отметим, что при μlt;tgα неравенство теряет смысл, и брусок не сможет ни при каких F, покоиться на плоскости, в ином случае это будет возможно при некоторых малых значениях силы F, и ускорение будет 0. Если брусок движется, то

Наконец вернемся к случаю, когда сила отрывает брусок от клина. Тогда у тела будет горизонтальное ускорение F/m и вертикальное g, поэтому полное ускорение составит

Соберем ответ
1)


2)

2a)
μlt;tgα

2b)
μ gt;= tgα
2b-1)

a = 0
2b-2)

такой же ответ как и в 2а
Спроецируем все силы на ось, перпендикулярную плоскости, предполагая, что тело все-таки лежит на ней, а не отрывается от нее внешней силой F
Итак, поскольку сила реакции опоры не может быть меньше нуля, находим первое ограничение на силу F
Поработаем в этом режиме. Сила F и сила тяжести стремятся двигать брусок вниз вдоль плоскости, значит сила трения направлена вверх вдоль плоскости. Тут также возможны два случая - тело покоится и тело стоит. Найдем в каком случае тело будет покоиться.
Сила трения не может превышать μN, поэтому
Отметим, что при μlt;tgα неравенство теряет смысл, и брусок не сможет ни при каких F, покоиться на плоскости, в ином случае это будет возможно при некоторых малых значениях силы F, и ускорение будет 0. Если брусок движется, то
Наконец вернемся к случаю, когда сила отрывает брусок от клина. Тогда у тела будет горизонтальное ускорение F/m и вертикальное g, поэтому полное ускорение составит
Соберем ответ
1)
2)
2a)
μlt;tgα
2b)
μ gt;= tgα
2b-1)
a = 0
2b-2)
такой же ответ как и в 2а
48
Смежные вопросы:
