Пожалуйста помогите........................

Question

Алгебра

Radedlel

6 год назад

Пожалуйста помогите........................

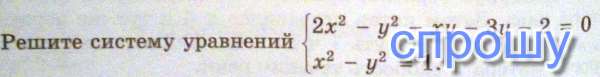
ОТВЕТЫ

Вениаминович

Jul 7, 2019

$\left\{\begin{array}{l} 2x^2-y^2-xy-3y-2=0 \\ x^2-y^2=1 \end{array}$

Попробуем разложить левую часть первого уравнения на множители:
$2x^2-y^2-xy-3y-2=0 amp;#10;\\\amp;#10;2x^2-yx-(y^2+3y+2)=0 amp;#10;\\\amp;#10;D=(-y)^2-4\cdot2\cdot(-(y^2+3y+2))=y^2+8y^2+24y+16=amp;#10;\\\amp;#10;=9y^2+24y+16=(3y+4)^2amp;#10;\\\amp;#10;x_1= \frac{y+(3y+4)}{2\cdot2} =y+1amp;#10;\\\amp;#10;x_2= \frac{y-(3y+4)}{2\cdot2} =- \frac{y}{2} -1amp;#10;\\\amp;#10;\Rightarrow 2x^2-y^2-xy-3y-2=2(x-y-1)(x+ \frac{y}{2} +1)amp;#10;\\\amp;#10;\Rightarrow 2x^2-y^2-xy-3y-2=(x-y-1)(2x+y +2)$

Система принимает вид:
$\left\{\begin{array}{l} (x-y-1)(2x+y +2)=0 \\ x^2-y^2=1 \end{array}$

Система распадается на две. Решаем первую:
$\left\{\begin{array}{l} x-y-1=0 \\ x^2-y^2=1 \end{array}$
$\left\{\begin{array}{l} x=y+1 \\ (y+1)^2-y^2=1 \end{array}$
$y^2+2y+1-y^2=1amp;#10;\\\amp;#10;2y=0amp;#10;\\\amp;#10;y_1=0amp;#10;\\\amp;#10;\Rightarrow x_1=0+1=1$

Решаем вторую систему:
$\left\{\begin{array}{l} 2x+y +2=0 \\ x^2-y^2=1 \end{array}$
$\left\{\begin{array}{l} y =-2x-2 \\ x^2-(-2x-2)^2=1 \end{array}$
$x^2-4x^2-8x-4=1 \\\ -3x^2-8x-5=0 \\\ 3x^2+8x+5=0 \\\ x_2=-1 \Rightarrow y_2=-2\cdot (-1)-2=2-2=0 \\\ x_3=- \frac{5}{3} \Rightarrow y_3=-2\cdot(-\frac{5}{3})-2= \frac{10}{3} - \frac{6}{3} = \frac{4}{3}$

Ответ: (1; 0); (-1; 0); (-5/3; 4/3)

170