1)Помогите найти число корней в следующем уравнении:

2) Помогите решить уравнение:

1) ОДЗ: 1≤х≤4
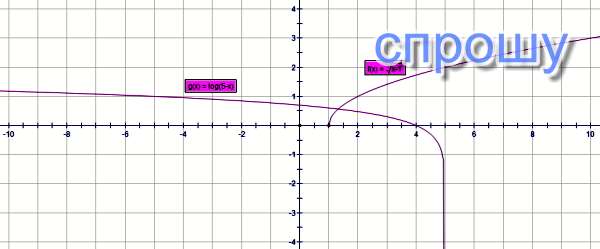
решение - графическое...
нужно ведь не корни найти, а количество корней)))
одна функция монотонно убывает, другая монотонно возрастает,
они если и пересекутся, то всего лишь ОДИН раз.
Ответ: один корень
2) ОДЗ: хgt;0; x≠1
(log(5)x)³ + 3(log(5)x)² = -2*log(5)x 
использована формула перехода к логарифму по новому основанию
(log(5)x)³ + 3(log(5)x)² + 2*log(5)x = 0
log(5)x*((log(5)x)² + 3*log(5)x + 2) = 0
1. log(5)x = 0 ---gt; x=1 ---посторонний корень (вне ОДЗ)
в скобках --квадратное уравнение относительно log(5)x
по т.Виета корни (-2) и (-1)
log(5)x = -2 ---gt; x₁ = 0.04
log(5)x = -1 ---gt; x₂ = 0.2