
Zhalabnas
7 год назад
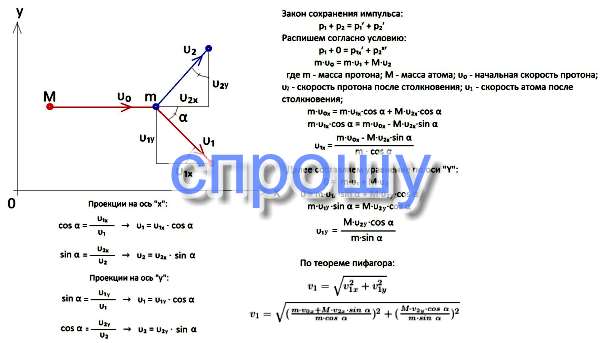
Протон, летящий со скоростью V0, упруго столкнувшись с неподвижным атомом, отклоняется на угол α. Скорость протона после столкновения уменьшается до V1. Определите скорость атома после удара.
прошу рассмотреть релятивистский случай
ОТВЕТЫ

Эммануил
Jul 5, 2019
Пусть M - масса атома, P - его импульс после столкновения
Закон сохранения импульса справедлив и в релятивистском случае (запишем векторно)

Выразим скорость атома из формулы для рел. импульса и подставим рел. импульсы протона до и после
![\displaystyleamp;#10;P^2 = \frac{M^2v^2}{1-v^2/c^2}\\\\amp;#10;v^2(P^2/c^2+M^2) = P^2\\amp;#10;v^2(1/c^2+M^2/P^2) = 1\\amp;#10;v = \left[1/c^2+m^2/P^2\right]^{-1/2} = \\\\amp;#10;= \left(\frac{M^2}{\frac{m^2v_1^2}{1-v_1^2/c^2}+\frac{m^2v_0^2}{1-v_0^2/c^2} - 2\frac{m^2v_0v_1}{\sqrt{1-v_0^2/c^2}\sqrt{1-v_1^2/c^2}}\cos\alpha}+\frac{1}{c^2}\right)^{-1/2}amp;#10; \displaystyleamp;#10;P^2 = \frac{M^2v^2}{1-v^2/c^2}\\\\amp;#10;v^2(P^2/c^2+M^2) = P^2\\amp;#10;v^2(1/c^2+M^2/P^2) = 1\\amp;#10;v = \left[1/c^2+m^2/P^2\right]^{-1/2} = \\\\amp;#10;= \left(\frac{M^2}{\frac{m^2v_1^2}{1-v_1^2/c^2}+\frac{m^2v_0^2}{1-v_0^2/c^2} - 2\frac{m^2v_0v_1}{\sqrt{1-v_0^2/c^2}\sqrt{1-v_1^2/c^2}}\cos\alpha}+\frac{1}{c^2}\right)^{-1/2}amp;#10;](https://tex.z-dn.net/f=5Cdisplaystyle0AP5E2+3D+5Cfrac7BM5E2v5E27D7B1-v5E22Fc5E27D5C5C5C5C0Av5E228P5E22Fc5E22BM5E229+3D+P5E25C5C0Av5E22812Fc5E22BM5E22FP5E229+3D+15C5C0Av+3D+5Cleft5B12Fc5E22Bm5E22FP5E25Cright5D5E7B-12F27D+3D+5C5C5C5C0A3D+5Cleft285Cfrac7BM5E27D7B5Cfrac7Bm5E2v_15E27D7B1-v_15E22Fc5E27D2B5Cfrac7Bm5E2v_05E27D7B1-v_05E22Fc5E27D+-+25Cfrac7Bm5E2v_0v_17D7B5Csqrt7B1-v_05E22Fc5E27D5Csqrt7B1-v_15E22Fc5E27D7D5Ccos5Calpha7D2B5Cfrac7B17D7Bc5E27D5Cright295E7B-12F27D0A)
Закон сохранения импульса справедлив и в релятивистском случае (запишем векторно)
Выразим скорость атома из формулы для рел. импульса и подставим рел. импульсы протона до и после
Для нерелятивистского случая
36
Смежные вопросы:
