
Thetamand
7 год назад
1)найдите сумму первых 29 членов арифметической прогрессии -3,5 -3,7
2)сколько первых членов арефметической прогрессии -12;-10;-8 нужно сложить чтобы получилось -30
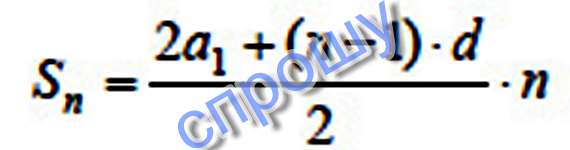
ОТВЕТЫ

Baevep
Jul 1, 2019
• Задание 1
Дано:
a(1) = -3,5;
a(2) = -3,7;
S(29) —
Решение:
#1 gt; Разность арифметической прогрессии:
d = a(2) - a(1) = -3,7 - (-3,5) = -0,2.
#2 gt; 29-ый член прогрессии:
a(29) = a(1) + d(29 - 1) = -3,5 - 28*0,2 = -9,1.
#3 gt; Сумма 29 первых членов:
S(29) = ((a(1) + a(29))/2) * n = ((-3,5 + (-9,1))/2) * 29 = -182,7.
Ответ: -182,7.
• Задание 2
Дано:
a(1) = -12;
a(2) = -10;
a(3) = -8;
S(n) = -30;
n —
Решение:
#1 gt; Разность арифметической прогрессии:
d = a(2) - a(1) = -10 - (-12) = 2.
#2 gt; Находим n:
S(n) = ((2*а(1) + d(n - 1))/2) * n = 30,
((2*(-12) + 2*(n - 1))/2) * n = 30,
n(-12 + n - 1) = 30,
n(-13 + n) = 30,
-13n + n² = 30,
n² - 13n - 30 = 0,
D = 13² - 4*(-30) = 169 + 120 = 289 = 17²,
n = (13 ± 7)/2,
n1 = 3, n2 = 10.
Ответ: 3 и 10.
Дано:
a(1) = -3,5;
a(2) = -3,7;
S(29) —
Решение:
#1 gt; Разность арифметической прогрессии:
d = a(2) - a(1) = -3,7 - (-3,5) = -0,2.
#2 gt; 29-ый член прогрессии:
a(29) = a(1) + d(29 - 1) = -3,5 - 28*0,2 = -9,1.
#3 gt; Сумма 29 первых членов:
S(29) = ((a(1) + a(29))/2) * n = ((-3,5 + (-9,1))/2) * 29 = -182,7.
Ответ: -182,7.
• Задание 2
Дано:
a(1) = -12;
a(2) = -10;
a(3) = -8;
S(n) = -30;
n —
Решение:
#1 gt; Разность арифметической прогрессии:
d = a(2) - a(1) = -10 - (-12) = 2.
#2 gt; Находим n:
S(n) = ((2*а(1) + d(n - 1))/2) * n = 30,
((2*(-12) + 2*(n - 1))/2) * n = 30,
n(-12 + n - 1) = 30,
n(-13 + n) = 30,
-13n + n² = 30,
n² - 13n - 30 = 0,
D = 13² - 4*(-30) = 169 + 120 = 289 = 17²,
n = (13 ± 7)/2,
n1 = 3, n2 = 10.
Ответ: 3 и 10.
1
