
Лобачевский
6 год назад
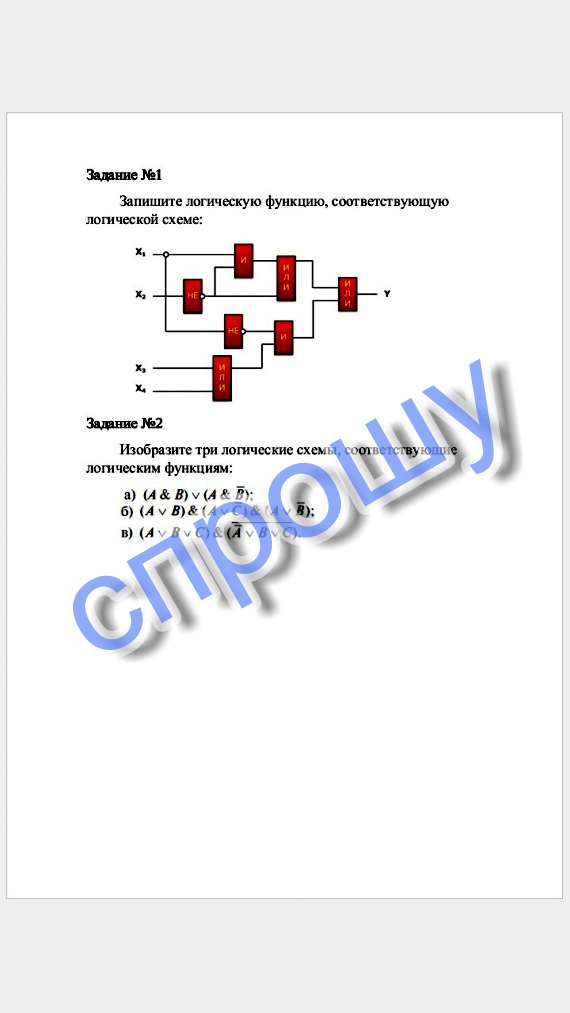
Помогите с информатикой Т-Т
ОТВЕТЫ

Досифей
Jul 1, 2019
1) Получение функции показано во вложении 1. Её имеет смысл немного упростить.


Схему рисовать смысла нет - сигнал А просто передается на выход.

И здесь "схема" аналогична предыдущему случаю.

Схема приведена во вложении 2.
Схему рисовать смысла нет - сигнал А просто передается на выход.
И здесь "схема" аналогична предыдущему случаю.
Схема приведена во вложении 2.
212
Смежные вопросы:
