Даны функции:
а) f: R→R, f(x) = 3x^2-x-2;
б) g: R→R, g(x) = -x^2+2x-3.
Найдите множество значений x€R, при которых f(x)>0 (f(x)<0) и g(x)>0 (g(x)<0).
пожалуйста, выручайте(

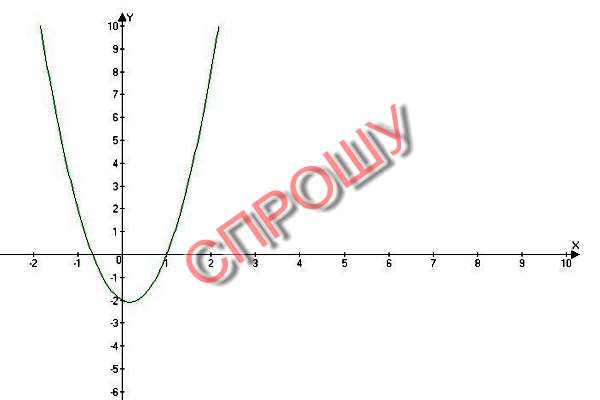
F(x) = 3x^2 -x -2.
Построим квадратичную функцию. Графиком функции является парабола, ветви направлены вверх, т.к. 3gt;0.

Координаты вершины параболы:

x = -b/2a = 1/(2*3) = 1/6.

y=3 * (1/6)^2 - 1/6 - 2 = - 25/12


И найдем корни уравнения

D=b^2-4ac = 1 + 24 = 25

x1 = -2/3
x2 = 1

Видим, что парабола пересекает ось Ох в точке x=-2/3 и x=1

Найдем множество значений х, при которых:

а) f(x)gt;0
  x ∈ (-∞;-2/3)∪(1;+∞)

б) f(x)lt;0
   x ∈ (-2/3;1).

g(x) = -x^2 + 2x - 3

Найдем координаты вершины параболы(ветви параболы направлены вниз, т.к. -1lt;0)

x = -b/2a = -2/(-2) = 1

y = -1 + 2*1 - 3  = -2

(1;-2) - координаты вершины параболы.

Найдем множество значений х, при которых:

а) g(x)gt;0

Видим, что нет таких х

б) g(x) lt; 0

А здесь х - любое. Можно сделать так (x-1)²+2lt;0