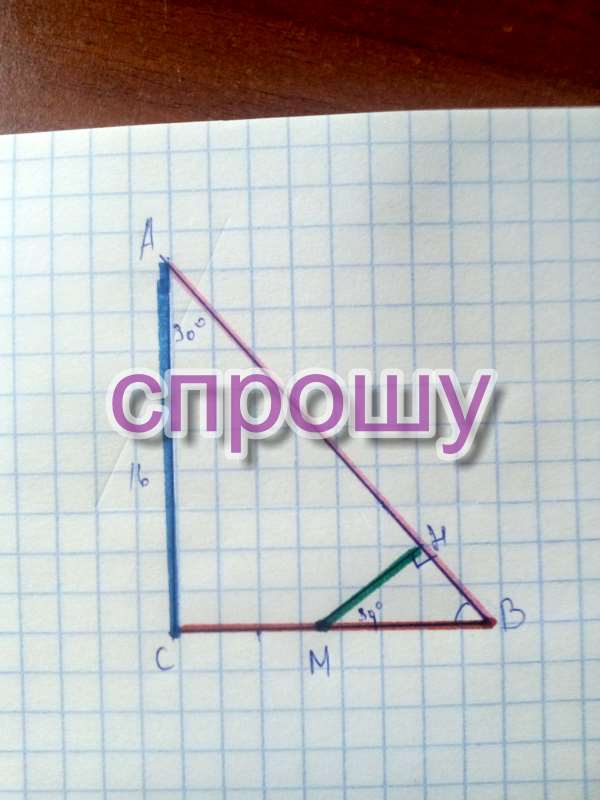
В прямоугольном треугольнике ABC угол C = 90 гр., угол A = 30 гр., AC = 16 см. Точка М - середина катета BC. Найдите расстояние от точки М до гипотенузы AB.

Т.к. ∠A = 30°, то CB = 1/2AB, т.к. напротив угла в 30° лежит катет, равный половине гипотенузе.
По теореме Пифагора:
AC² = AB² - CB²
256 = 4CB² - CB²
256 = 3CB²
CB² = 256/3
CB = 16√3/3 см.

MB = 1/2CB = 8√3/3 см - по условию.
∠B = 90° - ∠A = 90° - 30° = 60°.
∠MBH = 90° - ∠B = 90° - 60° = 30°.
Тогда HB = 1/2MB
HB = 1/2•8√3/3 см = 4√3/3 см.

По теореме Пифагора:
MH² = MB² - HB²
MH² = 64/3 - 16/3
MH² = 48/3
NH² = 16
MH = 4 см.

Ответ: 4 см.