Хотя бы одну!!! Даю 20 баллов!

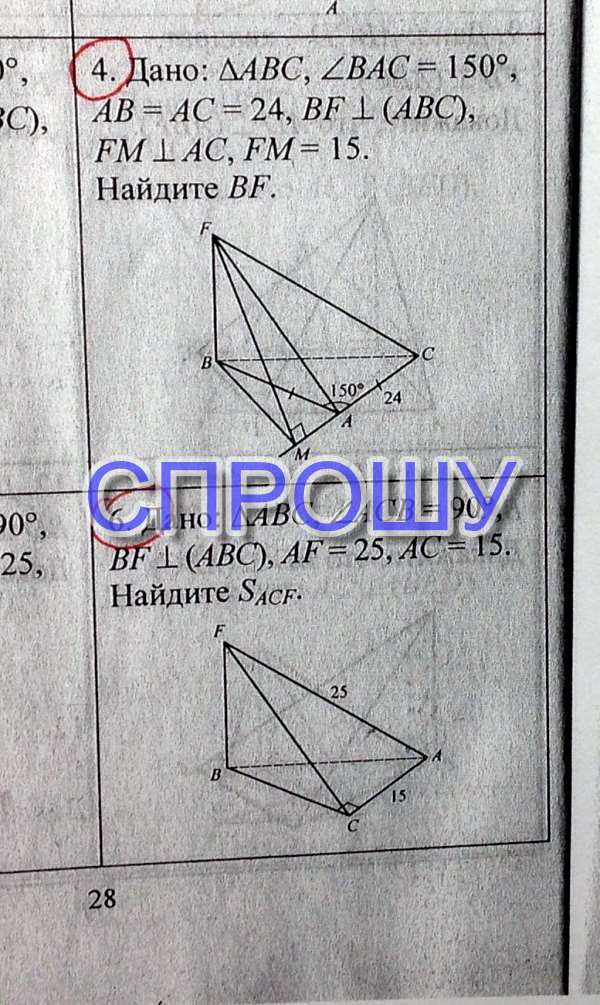
№4. BF_|_(ABC), FM_|_AC, =gt;BM_|_MC (теорема о трех перпендикулярах).
BF - перпендикуляр к плоскости треугольника
FM - наклонная
 BM - проекция наклонной на плоскости
МС - прямая, проведенная на плоскости через основание наклонной
Δ ВМА: lt;BAM= 30° (180°-150°=30° смежные углы)
lt;MBA=60° (90°-30°=60°)
BM=BA/2, катет против угла 30°
ВМ=12
ΔFBM: FM=15, BM=12
по теореме Пифагора:
FM²=BM²+BF²
15²=12²+BF²

BF=9

6. BF_|_(ABC)
FС - наклонная
FВ - перпендикуляр к плоскости
BC - проекция наклонной
AC - прямая на плоскости, перпендкулярная проекции наклонной
=gt; теорема о трех перпендикулярах
lt;FCA=90°
ΔFCA: по теореме Пифагора
FC²=25²-15²
FC=20
SΔACF=FC*AC/2
SΔ=(15*20)/2

SΔACF=150