Вычислите площадь фигуры, ограниченной линиями функций y = -x^2-4x, y = x+4.

Question

Алгебра

Thorius

6 год назад

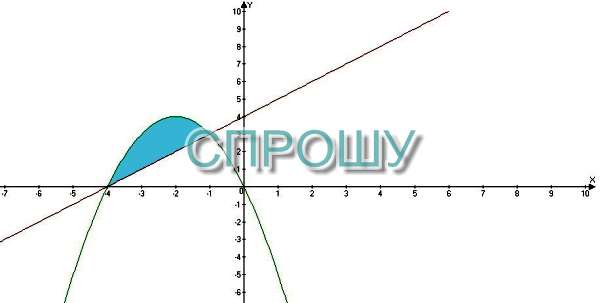
Вычислите площадь фигуры, ограниченной линиями функций y = -x^2-4x, y = x+4.

ОТВЕТЫ

Sonazhaks

Jun 29, 2019

Y=-x^2-4x - график парабола, ветви направлены вниз.

у=х+4 - прямая, проходящая через точки (0;4), (-4;0).

Площадь фигуры:

$\int\limits^{-1}_{-4} {(-x^2-4x-x-4)} \, dx = \int\limits^{-1}_{-4} {(-x^2-5x-4)} \, dx =\\ \\ =(- \frac{x^3}{3} -5\cdot \frac{x^2}{2}-4x)|^{-1}_{-4}= \frac{9}{2}$

Найдем пределы интегрирования
-x²-4x=x+4
x²+5x+4=0
x1+x2=-5 U x1*x2=4⇒x1=-4 U x2=-1
Фигура ограничена сверху параболой,а снизу прямой
$S= \int\limits^{-1}_{-4} {(-x^2-5x-4)} \, dx =-x^3/3-5x^2/2-4x|-1-(-4)=$ $1/3-5/2+4-64/3+40-16=4,5$

170