
Manasida
7 год назад
Помогите решить уравнения и неравенства, пожалуйста. Продам душу за решение хотя бы нескольких логов ♥
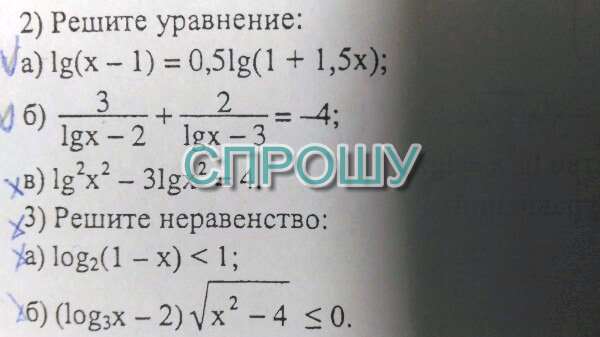
ОТВЕТЫ

Epifaniy
Jun 29, 2019
2.
a) lg(x-1)=0,5*lg(1+1,5x) |×2
ОДЗ: x-1gt;0 xgt;1 1+1,5xgt;0 xgt;-2/3 ⇒ x∈(1;+∞)
2*lg(x-1)=lg(1+1,5x)
lg(x-1)²=lg(1+1,5x)
(x-1)²=1+1,5x
x²-2x+1=1+1,5x
x²-3,5x=0
x*(x-3,5)=0
x₁=0 ∉ОДЗ x=3,5.
б) 3/(lgx-2)+2/(lgx-3)=-4
3*lgx-9+2lgx-4=-4lg²x+4*5lgx-4*6 ОДЗ: xgt;0
5lgx-13=-4lg²x+20lgx-24
4lg²x-15lgx+11=0
lgx=t
4t²-15t+11=0 D=49
t₁=1 lgx=1 x₁=10
t₂=2,75 lgx=2,75 x₂=10^(2,75).
lg²x²-3*lgx²=4
lgx²=t
t²-3t-4=0 D=25
t₁=4 lgx²=4 x²=10⁴ x₁=100 x₂=-100
t₂=-1 lgx²=-1 x²=10⁻¹=0,1 x₃=√0,1 x₄=-√0,1.
3.
a) log₂(1-x)lt;1 ОДЗ: 1-xgt;0 xlt;1
log₂(1-x)lt;log₂2
1-xlt;2
xgt;-1 ⇒ Согласно ОДЗ:
x∈(-1;1).
б) (log₃x-2)*√(x²-4)≤0
ОДЗ: xgt;0 x²-4≥0 (x+4)(x-4)≥0 -∞____+____-4____-____4____+____+∞
x∈(-∞;-4]U[4;+∞) ⇒ x∈[4;+∞).
Так как √(x²-4)≥0 ⇒
log₃x-2≤0
log₃x≤2
log₃x≤log₃9
x≤9 ⇒ Согласно ОДЗ:
x∈[4;9].
a) lg(x-1)=0,5*lg(1+1,5x) |×2
ОДЗ: x-1gt;0 xgt;1 1+1,5xgt;0 xgt;-2/3 ⇒ x∈(1;+∞)
2*lg(x-1)=lg(1+1,5x)
lg(x-1)²=lg(1+1,5x)
(x-1)²=1+1,5x
x²-2x+1=1+1,5x
x²-3,5x=0
x*(x-3,5)=0
x₁=0 ∉ОДЗ x=3,5.
б) 3/(lgx-2)+2/(lgx-3)=-4
3*lgx-9+2lgx-4=-4lg²x+4*5lgx-4*6 ОДЗ: xgt;0
5lgx-13=-4lg²x+20lgx-24
4lg²x-15lgx+11=0
lgx=t
4t²-15t+11=0 D=49
t₁=1 lgx=1 x₁=10
t₂=2,75 lgx=2,75 x₂=10^(2,75).
lg²x²-3*lgx²=4
lgx²=t
t²-3t-4=0 D=25
t₁=4 lgx²=4 x²=10⁴ x₁=100 x₂=-100
t₂=-1 lgx²=-1 x²=10⁻¹=0,1 x₃=√0,1 x₄=-√0,1.
3.
a) log₂(1-x)lt;1 ОДЗ: 1-xgt;0 xlt;1
log₂(1-x)lt;log₂2
1-xlt;2
xgt;-1 ⇒ Согласно ОДЗ:
x∈(-1;1).
б) (log₃x-2)*√(x²-4)≤0
ОДЗ: xgt;0 x²-4≥0 (x+4)(x-4)≥0 -∞____+____-4____-____4____+____+∞
x∈(-∞;-4]U[4;+∞) ⇒ x∈[4;+∞).
Так как √(x²-4)≥0 ⇒
log₃x-2≤0
log₃x≤2
log₃x≤log₃9
x≤9 ⇒ Согласно ОДЗ:
x∈[4;9].
246
Смежные вопросы:
