
Агафоник
6 год назад
Как можно разложить cos4x?
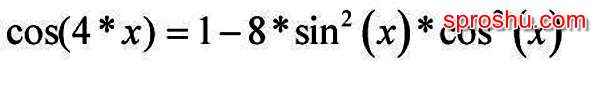
ОТВЕТЫ

Joshua
Oct 2, 2019
Разложить cos(4*x) можно двукратным применением формулы для косинуса двойного аргумента. Сделаем замену переменной: a=2*x, тогда получится cos(2*x)=cos(a).
Формула для косинуса двойного аргумента:
cos(2*a)=cos^2(a)-si
Далее переходим к переменной x и получаем:
cos(4*x)=cos^2(2*x)-
=1-2*2*sin(x)*cos(x)
Итог:
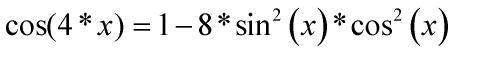
198
