Сколько существует трехзначных чисел с суммой цифр, делящейся на 13?

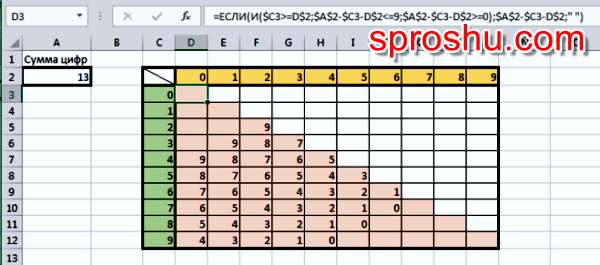
Очевидно, что максимальная сумма которая может быть достигнута, это 9+9+9=27.

Для того чтобы сумма делилась на 13, она должна быть равная 13 или 26. Это может быть достигнуто при определенном сочетании цифр.

Попробуем составить небольшой расчет в экселе.

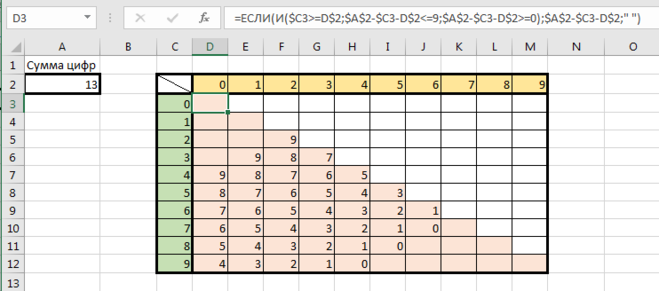
Сумма цифр в обозначениях строк, столбцов и значении в таблице равна 13. За счет организации рабочего треугольника, некоторые повторы можно исключить, но третье число в таблице может создавать повтор со строками или столбцами. Поэтому сделаем творческую выборку вариантов.

Варианты где все цифры разные.

139 148 157 238 247 256 346

Семь вариантов набора цифр. Каждый набор даст шесть вариантов перестановок.

7х6=42

Варианты с повтором цифр.

166 229 337 355 445

Пять вариантов набора цифр. Каждый набор даст три варианта перестановок.

5х3=15

Варианты с нулем.

049 058 067

Три варианта набора цифр. Ноль не может находится в старшем разряде, поэтому четыре варианта перестановок.

3х4=12

Для суммы цифр равное 26 существует только один вариант набора цифр.

899

Число перестановок равное трем.

1х3=3

Итого получаем 42+15+12+3=72 варианта трехзначных чисел.