Можно ли построить такую треугольную пирамиду?

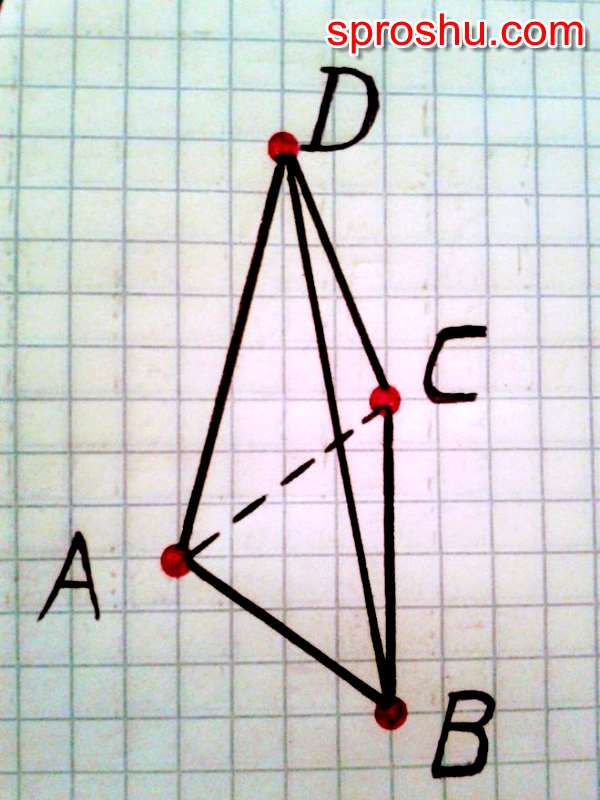
Да, такую пирамиду построить можно. Доказательство.

Расположим на произвольной плоскости в произвольном порядке три точки А, В, С, не лежащие на одной прямой, и соединим их между собой. Получим треугольник АВС. Далее, над этой плоскостью произвольным образом расположим точку D. Эту точку соединим с каждой из вершин полученного треугольника АВС.

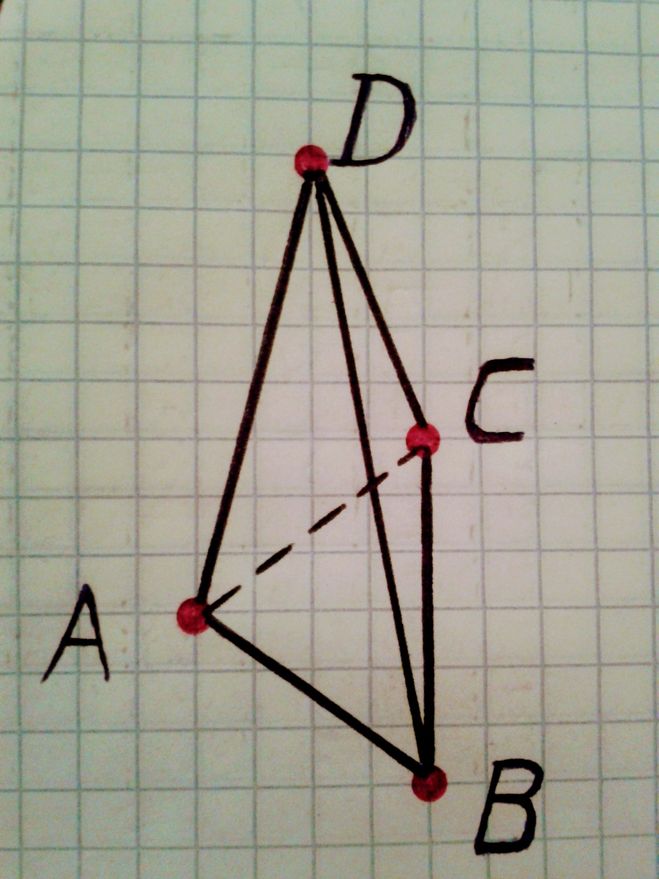
В результате получим пирамиду ABCD.

1-й способ.

Точку D всегда можно расположить так, чтобы длины двух рёбер, сходящихся в ней, например, рёбер AD и CD, удовлетворяли бы условиям данной задачи, а именно:

AD≥AC+AB,

CD≥CA+CB.

Когда точка D выбрана и соединена с вершинами A и C ∆ABC, остаётся только расположить плоскость ADC под таким углом φ к плоскости ABC, чтобы длина ребра BD удовлетворяла условиям задачи, а именно:

BD≥BA+BC,

DB≥DA+DC.

Но из неравенств треугольника следует, что

AB+BC>AC,

AD+CD>AC.

Сложив последние четыре неравенства, получим:

BD+BD+AB+BC+AD+CD>AB­+BC+AD+CD+AC+AC, или

BD>AC.

Последнее неравенство всегда можно выполнить, если найти соответствующий двугранный угол между плоскостями ABC и ACD.

2-й способ.

Пусть указанная пирамида существует. Тогда для рёбер, входящих в вершины ∆ABC, выполняются условия:

AD≥AB+AC,

BD≥AB+BC,

CD≥AC+BC.

BD≥AD+CD.

Сложив указанные неравенства, получим:

AD+CD+2•BD≥2•(AB+AC+­BC)+AD+CD, или

BD≥AB+AC+BC=p, где p — периметр ∆ABC.

Таким образом, для существования пирамиды с указанными в условиях задачи свойствами её рёбер, достаточно, чтобы выполнялось последнее неравенство, т. е., длина одного из рёбер пирамиды, не лежащего в одной плоскости с тремя другими её рёбрами, должна быть больше или равна периметру треугольника, образуемого этими тремя рёбрами.

Периметр ∆ABC можно сделать сколь угодно малым, а длину ребра BD сколь угодно большой, чтобы пирамида с указанными свойствами существовала.