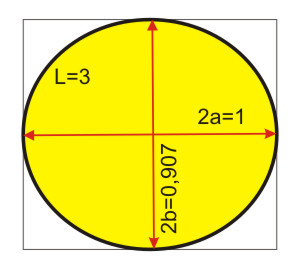
Как построить овал, в котором малая ось в 3 раза меньше окружности?

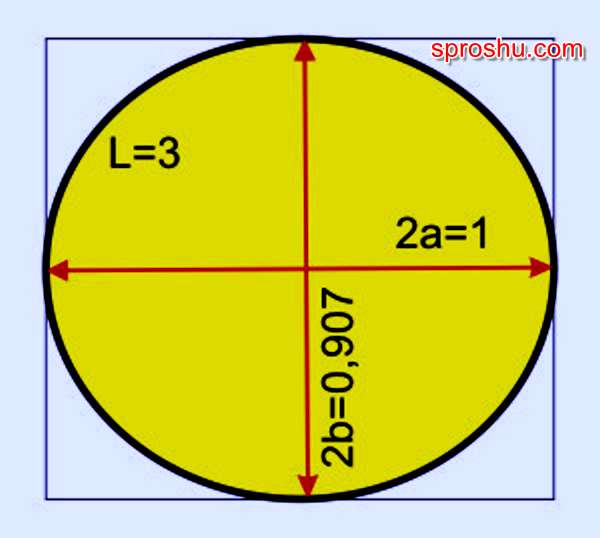
Все достаточно просто.

Формула периметра эллипса L=2*pi*sqrt((a^2-b­^2)/2),

где а и b - полуоси эллипса.

(sqrt - квадратный корень, ^ - степень, pi - число Пи).

Чтобы найти соотношение осей эллипса, при котором длина его периметра будет равна 3 длинам одной из осей, нужно подставить в эту формулу вместо L трехкратную длину одной из осей. Если полуось - это а, то вся ось = 2а.

Трехкратная ее длина будет 3*2а=6а.

Получим формулу:

6*а=2*pi*sqrt((a^2­-b^2)/2),

решим эту формулу относительно полуоси b.

Получим:

b=sqrt(18/pi^2-1)*­a

b=0,907*a.

То есть получаем легкую сплюснутость окружности примерно в отношении 0,9 до эллипса, при которой одна из его осей (по факту большая) равняется точно одной третьей части его периметра.

Если же малую полуось b принять за 1, то большая полуось а относительно нее будет

а=1/0,907=1,102.

В любом случае длина периметра эллипса оказывается в три раза больше не короткой, а длинной оси. Вид у эллипса будет примерно такой.!