Текстовая задача. Как вычислить ширину реки?

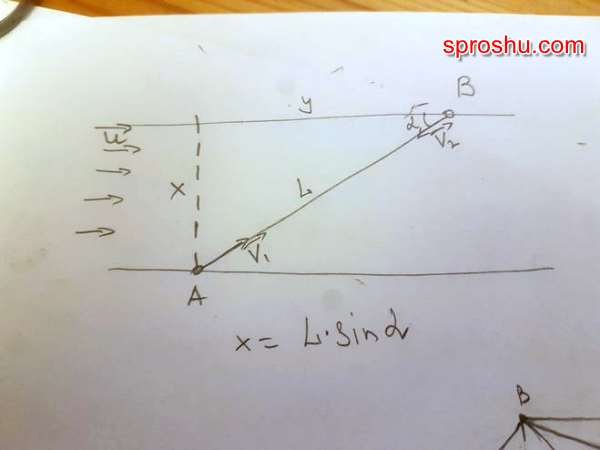
Дано:

Расстояние между пунктами А и В = 50 км

Скорость лодки U = 32 км/ч

Скорость течения u = 5 км/ч

Разница во времени τ=0,5ч

Найти расстояние между берегами, время и скорость поездок - ?

Итак, если мы найдем X=L*sinα то решим задачу.

Построим векторную схему скоростей (рис 2):

V1 - скорость по течению, V2 - против.

Угол α так же присутствует.

Нарисуем схему скоростей отдельно, совместив их в точке D=D’=D" на одном рисунке, получим параллелограмм A"ВСD, CD=u, A"В=u, BD=U.

A’C=U , а треугольник △А’ВD=△А’CD - по стороне и углу.

Значит А’BCD - равнобедренная трапеция, А’В = u, а △ А’ВА" - равнобедренный, ВА=h - высота.

Решение:

τ=L/V2-L/V1

τ=L((V1-V2)/(V1V2))

V1-V2=2*△V=2u*cosα

AA’=AA"=△V => AD=K, V1=K+△V, V2=K-△V

K^2=U^2-h^2=U^2-(u^2­-△V^2)=U^2-u^2+△V^2

τ=L(2u*cosα/(K^2-△V^­2))

τ=L(2u*cosα/(U^2-u^2­+△V^2-△V^2))

τ=L(2u*cosα/(U^2-u^2­)

cosα=τ(U^2-u^2)/(2uL­)=999/1000

α~2,56°

X=2,23 км.

K~32

△V=4,995

V1~37

V2~27

t1~1.352

t2~1.852

Возможно, решается проще+_+