
Вариант 19. Задание 9. Как найти значение логарифмического выражения?
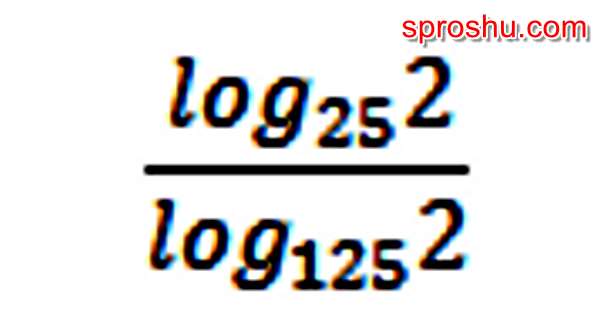

Предложу два способа решения, они опираются на применение различных свойств логарифма. Сразу пояснение по оформлению: в скобках после логарифма указано его основание, a^n - классическое обозначение "а в степени n".
1 способ.
Для начала, надо преобразовать числитель и знаменатель.
Числитель:
log(25)2=log(5^2)2=1
Знаменатель:
log(125)2=log(5^3)2=
Соответственно, логарифм log(5)2, находящийся и в числителе, и в знаменателе, сокращается, остаётся выражение:
1/2 : 1/3 = 3/2
2 способ.
По свойству логарифма, имеем:
log(a)b = 1/log(b)a
Используя это правило, поменяем числитель и знаменатель местами, поменяв местами a и b а каждом логарифме. Получим:
log(2)125/log(2)25
Применяем формулу перехода к новому основанию:
log(2)125/log(2)25=l
Ответ: 3/2
автор вопроса выбрал этот ответ лучшим