Вариант 19. Задача 13. Чему равен объем отсеченного конуса?

Объем конуса - это одна третья произведения площади основания на его высоту. Круг - основание конуса. (нам нужна площадь круга) Таким образхом объем

V = 1/3 Sоснования · h =1/3 ? D 2/4 · h

По рисунку

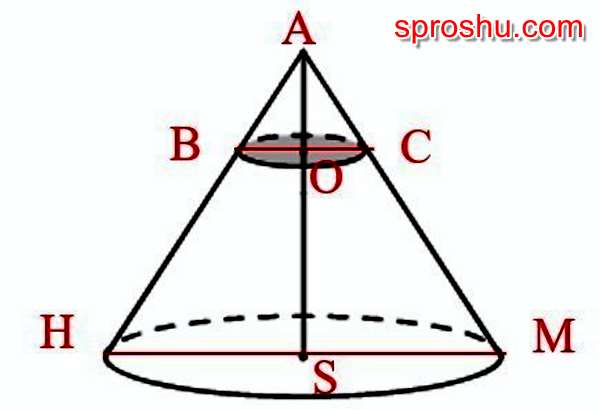
Треугольники АВС и АНМ – подобны по величине трех углов. Из этого следует:

ВС : НМ = AO : AS = 1 : 4 (известно по условию, что AO : OS = 1 : 3), получаем

НМ = 4ВС

AS = 4AO

Следовательно первоначально объем конуса:

V1 = 1/3 ?D2/4 · h = 1/3 ? · НМ2 · АS =1/3 ? · (4BC)2 · (4AO) = 512

Объём второго конуса (отсеченного) будет рассчитываться по формуле:

V2 = 1/3 ?D2/4 · h = 1/3 ? · ВС2 · AO

Найдем, во сколько раз объем большого конуса больше отсекаемого. Найдем отношение объема V1 конуса на V2 :

V1 / V2 = (1/3 ? · (4BC)2 · (4AO)) / (1/3 ? · ВС2 · AO) = в 64 раза объем большего конуса больше отсекаемого.

Найдем обьем, отсекаемого от первоначального конуса, плоскостью:

V2 = V1 / 64 = 512 / 64 = 8 см3.