Задача. Чему равен радиус окружности выписанной треугольник ABC (см)?

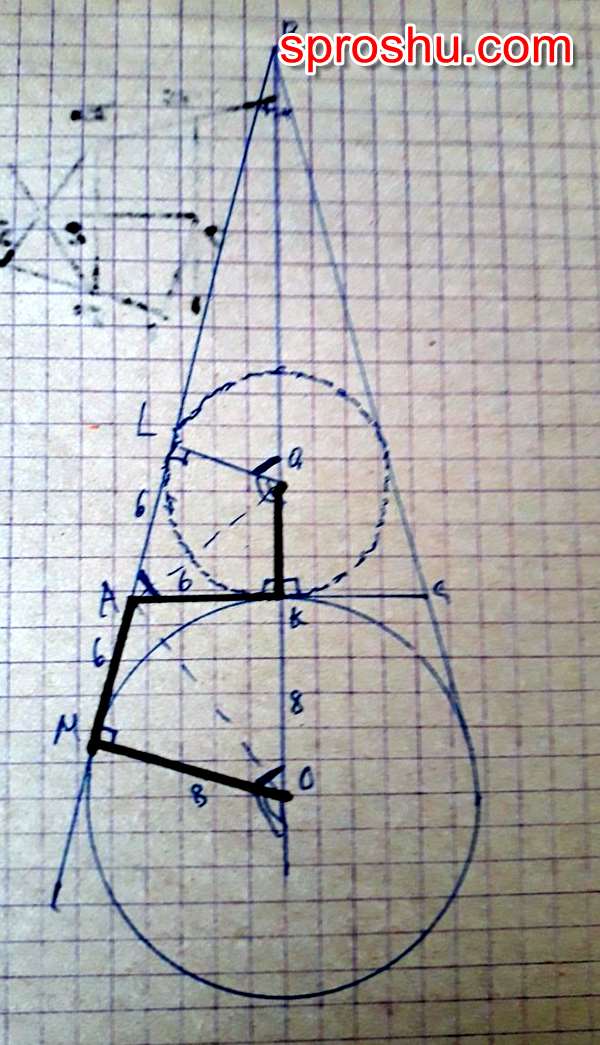
Начнём с построения заданных элементов чертежа. Начертим две взаимно перпендикулярные прямые: вертикаль, от низа листа до верха, и горизонталь, вдоль низа листа. Точку их пересечения обозначим О. От точки О отложим влево отрезок ОД и вверх ОК равные радиусу окружности, 8-ми единицам, например 8 см. Ещё отложим тоже влево отрезок ОЕ равный 6-ти см, половине основания AC равнобедренного треугольника ABC. От точки Е отложим вертикально вверх отрезок ЕА равный радиусу ОМ. Через точки Д и А проведём прямую до пересечения с вертикалью в точке В. Прямоугольные треугольники ДОВ и АМВ подобны как имеющие кроме прямого угла общий угол при вершине В. Из подобия этих треугольников следует ОВ/МВ=ОД/МА=8/6=4/3 Проводим биссектрису угла МАВ до пересечения с вертикалью в некоторой точке Х, а из этой точки проведём перпендикуляр ХЮ к АВ. Прямоугольные треугольники ХМА и ХЮА будут равны как имеющие равные острые углы и следовательно ХМ=ХЮ и следовательно Х является искомым центром окружности вписанной в треугольник АВС. Прямоугольные треугольники тоже подобны как имеющие кроме прямого угла ещё общую сторону МА=6. Из подобия этих прямоугольных треугольников следует МА/МХ=ОМ/МА=8/6=4/3 и МХ=3*МА/4=18/4=4,5.